Difference between revisions of "Hyperoperations Wiki"
m (MphLee moved page Main Page to Hyperoperations Wiki) |
|||
| (9 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | + | The [[Hyperoperations Wiki]] is intended to complement [http://math.eretrandre.org/tetrationforum/ the Tetrationforum]. By keeping track of the definitions, notations, ideas, and bibliographic references, it aims to create a ''cartographic tool'' for the exploration done at the [[Tetrationforum]]. Additionally, by formally re-expressing all modern mathematical concepts from a preparatory viewpoint that is compatible with ''hyperoperative'' inquiry, the wiki could help bridge the historical gap to contemporary mathematics. | |
| + | [[File:hw.png|250px|center]] | ||
| + | |||
| + | ==Idea== | ||
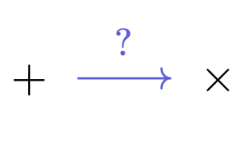
| + | [[File:hw_2.png|thumb|350px|right|The [[hyperoperations]] emerge from the investigation of the nature of [[arithmetical operations]].]] | ||
| + | |||
| + | Organizing the knowledge and folklore surrounding the [[tetration]] function, as well as the broader circle of ideas encompassed by the term "hyperoperation," presents two major challenges: | ||
| + | <ol style="list-style-type:lower-alpha"> | ||
| + | <li> most of the work done in this field is extremely heterogeneous in its style, notation, and often lacks reciprocal acknowledgment; </li> | ||
| + | <li> even when some degree of terminological consensus about the mathematical objects inquired is found, the unclear connection to well-known, standard mathematical theories and terminology leaves one with the doubt of reinventing the wheel or the concern of wasting time in fringe, crackpot mathematics. </li> | ||
| + | </ol> | ||
| + | Solving (a) would increase the internal unity of the field of hyperoperations bringing its fundamental problems into clearer view and allowing us to "focus" on them effectively, while solving (b) would provide access powerful and well-established theories and methods for the field. | ||
| + | |||
| + | The Hyperoperations Wiki serves as an online collaborative [[encyclopedia]] with a dual purpose. On one hand, it aims to map the [[definitions]] and [[relationships]] among the mathematical structures that emerge from and are connected to the [[abstract]] [[concept]] of [[hyperoperations]], effectively addressing problem (a). On the other hand, to ensure it is self-contained, the wiki should provide all fundamental definitions—logical, set-theoretical, algebraic, and geometric— in a manner that makes them directly applicable to structures derived from hyperoperations, presenting them from what could be termed a '''''hyperoperational perspective ([[hPOV]]).''''' Dually, this solves problem (b) by situating all the structures within the landscape of modern and contemporary [[mathematics]]. | ||
| + | |||
| + | ===The hPOV and the concept of iteration=== | ||
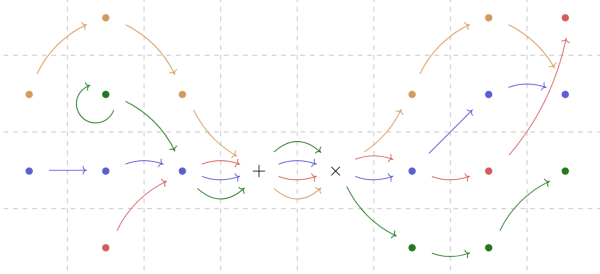
| + | Just like the concept of a [[ring]], the concept of hyperoperation serves as a potential avenue for exploring the conceptual nature of [[arithmetical operations]] through [[generalization]] and [[abstraction]]. The approach taken by the [[hPOV]] lies on the assumption that some of the relationships between addition and multiplication have a hierarchical nature: some of them are suggestive of an unidirectional increase in complexity and reveal pathways to explore further in those directions, '''''above and beyond''''', i.e. ''ὑπέρ ([[hyper]])'', '''''sums and products'''''. The path suggested is the one of '''''repetition''''', or '''''doing again, once more''''', i.e. ''iterum ([[iteration]])'' that step that got us from addition to multiplication. | ||
| + | |||
| + | [[File:hw_3.png|thumb|600px|center|Intuition about extending the conceptual relationship between sum and product to the whole space of operations.]] | ||
| + | |||
| + | There is a circular relation between the hPOV and the iterative point of view, a kind of duality. | ||
| + | * At first sight, it may seem that iteration supplies the natural ambient theory where to investigate hyperoperations. Once a process linking addition to multiplication is chosen, the study of Hyperoperations seems to be reduced to '''iterating''' that chosen process beyond them. | ||
| + | *Yet also the opposite is true. Iteration emerges naturally just as one of the many possible ways to understand the connection between addition and multiplication. | ||
| + | |||
| + | This reveals the possibility of an intersection of the two points of view by definition of a deeper and fundamental concept, an intersection where the ''iteration of iteration itself'' could happen. | ||
| + | |||
| + | |||
| + | ===Useful pages=== | ||
[[Special:AllPages]] brings you to a list of all so far described terms. | [[Special:AllPages]] brings you to a list of all so far described terms. | ||
Latest revision as of 12:37, 19 May 2025
The Hyperoperations Wiki is intended to complement the Tetrationforum. By keeping track of the definitions, notations, ideas, and bibliographic references, it aims to create a cartographic tool for the exploration done at the Tetrationforum. Additionally, by formally re-expressing all modern mathematical concepts from a preparatory viewpoint that is compatible with hyperoperative inquiry, the wiki could help bridge the historical gap to contemporary mathematics.
Idea
Organizing the knowledge and folklore surrounding the tetration function, as well as the broader circle of ideas encompassed by the term "hyperoperation," presents two major challenges:
- most of the work done in this field is extremely heterogeneous in its style, notation, and often lacks reciprocal acknowledgment;
- even when some degree of terminological consensus about the mathematical objects inquired is found, the unclear connection to well-known, standard mathematical theories and terminology leaves one with the doubt of reinventing the wheel or the concern of wasting time in fringe, crackpot mathematics.
Solving (a) would increase the internal unity of the field of hyperoperations bringing its fundamental problems into clearer view and allowing us to "focus" on them effectively, while solving (b) would provide access powerful and well-established theories and methods for the field.
The Hyperoperations Wiki serves as an online collaborative encyclopedia with a dual purpose. On one hand, it aims to map the definitions and relationships among the mathematical structures that emerge from and are connected to the abstract concept of hyperoperations, effectively addressing problem (a). On the other hand, to ensure it is self-contained, the wiki should provide all fundamental definitions—logical, set-theoretical, algebraic, and geometric— in a manner that makes them directly applicable to structures derived from hyperoperations, presenting them from what could be termed a hyperoperational perspective (hPOV). Dually, this solves problem (b) by situating all the structures within the landscape of modern and contemporary mathematics.
The hPOV and the concept of iteration
Just like the concept of a ring, the concept of hyperoperation serves as a potential avenue for exploring the conceptual nature of arithmetical operations through generalization and abstraction. The approach taken by the hPOV lies on the assumption that some of the relationships between addition and multiplication have a hierarchical nature: some of them are suggestive of an unidirectional increase in complexity and reveal pathways to explore further in those directions, above and beyond, i.e. ὑπέρ (hyper), sums and products. The path suggested is the one of repetition, or doing again, once more, i.e. iterum (iteration) that step that got us from addition to multiplication.
There is a circular relation between the hPOV and the iterative point of view, a kind of duality.
- At first sight, it may seem that iteration supplies the natural ambient theory where to investigate hyperoperations. Once a process linking addition to multiplication is chosen, the study of Hyperoperations seems to be reduced to iterating that chosen process beyond them.
- Yet also the opposite is true. Iteration emerges naturally just as one of the many possible ways to understand the connection between addition and multiplication.
This reveals the possibility of an intersection of the two points of view by definition of a deeper and fundamental concept, an intersection where the iteration of iteration itself could happen.
Useful pages
Special:AllPages brings you to a list of all so far described terms.